Asymptotic Notations Pt 2

Big O Notation
With the Big Theta notation we bound the growth of a runtime within a constant upper and lower factor. However, there are some times where we want to bound that growth to the upper factor. This is where the Big O notation comes in to play.

With binary search the worst case scenario is 𝛉(log2(n)), however, this is not the case 100% of the time as it is possible to find the target value on the first try which would make the runtime 𝛉(1). Therefore you can say that the runtime of binary search is never worse than 𝛉(log2(n)) but can be better. How would we write this using asymptotic notations, well we would write O(log2(n)).

Like with the big theta notation once n becomes large enough it is less than or equal to k * f(n), the big O notation can be used. Of course the Big O notation can also be used on any function and not just a logarithmic function.

Big Omega Notation

Sometimes we instead want to say that a runtime will take at least a certain amount of time, but without providing an upper bound. This is where the big omega notation comes into play. This means any function where n becomes large enough and is greater than or equal to k * f(n).

The Big Theta notation implies both Big O and Big Omega notations, but both Big O and Big Omega notations are imprecies due to not using both bounds. With this imprecision it is best to use Big Theta when describing a runtime of an algorithm.

Asymptotic Notations Pt 1

The runtime of any algorithm is decided by various factors such as the speed of the computer, the programming languages used, how long it takes for a compiler to translate the programming code into machine code and more.

We can think of the runtime of an algorithm as a function of the size of it's input. The makes sense when you look at linear or binary search algorithms because they take longer as you increase the size of the array that you are searching through.

We also need to think about the growth of the function as the size of the input increases, which is often referred to as the rate of growth. To make things more managable we simplify the function. This means removing the less important parts from the function. For example; we have the function 6n^2 + 100n + 300, where n is the size of the input. At some point the 6n^2 part of the function is going to become greater than 100n + 300 part, this actually happens when n = 20. Therefore we can get rid of the 100n + 300 part. We can also remove the 6 coefficient part of the 6n^2. This is because as long as the coefficient is > 0 then the difference will increase as does n. So we can say that the function grows as n^2.

By dropping the less important parts we can completely focus on the rate of growth of an algorithms runtime. When we do this we use asymptotic notations. Three examples of these types of notations are the big theta (𝛉), big O and big omega (𝛀).

Big Theta
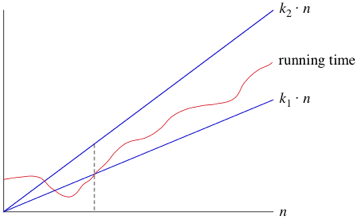
As mentioned before the runtime of an algorithm is made up of various factors (some listed above) this will be denoted as c1. Then we have the input size or number of loop iterations, which is denoted as n. Finally we have the overhead of a function such as initialising the index to 0, this is denoted as c2. Using these values we can calculate the total time for the worst case scenario (which in a linear search is not finding a value). The formula is c1 * n + c2.

Both c1 and c2 don't tell us anything about the rate of growth of the runtime. The important part is n and so because both c1 and c2 are also constants we can drop both of them. Therefore the notation we use for the worst case scenario of a linear search is 𝛉(n).
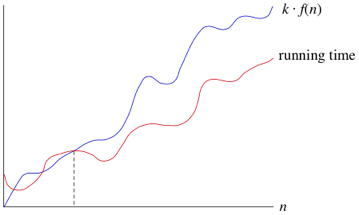
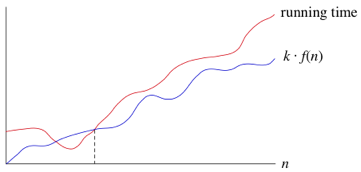
What this means is when n is large enough, the runtime is greater than k1 * n and less than k2 * n, where k1 and k2 are some constants. This can be seen in the graph below.

We can also use other functions of n, such as n^2 or nlog2. Therefore as long as any runtime that uses some function of n, f(n), is greater than k1 * f(n) and is less than k2 * f(n), it is a big theta notation or in other words 𝛉(f(n)).

Another advantage of using these notations means that we don't have to note the time units being used. So the previous example of 6n^2 + 100n + 300, becomes 𝛉(n^2). When we use this notation we are saying we have a asymptotically tight bound on the runtime. This is because it only matters when n is large enough (this gives us the asymptotically part) but also because the runtime is between the two k constants * f(n) (this gives us the tight bound part).

Growth Characteristics
There are 6 typical types of growth; constant, logarithmic, linear, linearithmic, polynomial and exponential, however, there are other types of growth that might not be covered.

An example of a constant growth is finding the first element within an array. The function would be 1 as element 0 is always the first element. An example of an logarithmic function is Log2(n). This means how many 2 we need to multiply to get n. Linear is where n (the size of the input) is multiplied by some sort of coefficient, for example 3n would have a linear growth. Linearithmic is a combination of logarithmic and linear functions. An example of this is nLog2(n). Polynomial is similar to linear but this time n has a power/indice that follows after it. For example 3n^2 or n^6. Finally there is exponential and this is where some number has an indice of n, for example (3/2)^n or 6^n.

The order of growth is:

1. Constant
2. Logarithmic
3. Linear
4. Linearithmic
5. Polynomial
6. Exponential

Its worth noting that with logarithmic and linearithmic functions the growth speed is dependant on the base, the lower the base value the quicker the growth. For example log2(n) is faster than log8(n). With polynomial and exponential functions, the higher value the power/indice is the quicker the growth. So n^2 is slower than n^4.

Precompiled Headers In C++

Usually when you include a header file in any C++ file, all of the contents of the header file is copied and compiled into the C++ file. This isn't so bad for a single header file, but if the header file also included several other header files, they also have to be compiled. So if you have a large project, you can expect the compile times to be very long without using precompiled headers. By precompiling headers, it converts a set of headers into a single file that uses the binary format in which the compiler can read and this is only done once. This however doesn't work if you add header files that you will be constantly or even occasionally changing as it means that the precompiled header now has to be recompiled every time a change is made.

Precompiled headers are usually used for headers that are going to be used often throughout the project such as the standard libary or any external libraries that you might be using. This is because they aren't going to change (unless there is a major issue with a version of an external library, which causes you to update that library). You can also use it for your own libraries but as mentioned above it is only worth doing if that library you have created is complete and isn't going to change or isn't likely to change.

There is a disadvantage to using precompiled headers and that is that it can hide the dependancies of a C++ file. Normally by just including whatever header files in a C++ file, you can easily tell what it requires. This means that if you were to reuse that C++ file within another project, you already know what else you will need if you don't already have it within that project. However, this is not the case with precompiled headers as it most likely has a ton of header files that are being used throughout the project but not specifically for the C++ file that you want to reuse. Therefore, if you did reuse that file you would have to figure out the header files that the file depends on.

Also if you are only going to use a header file in a single C++ file then it is not worth adding to the precompiled headers file. This is because that header file is more than likely going to be abstracted into your own api for you to use. An example of this would be the GLFW header file.

Below is a useful video on the subject, in which these notes are based on, but also the set up needed to use precompiled headers within a C++ project.