With the Big Theta notation we bound the growth of a runtime within a constant upper and lower factor. However, there are some times where we want to bound that growth to the upper factor. This is where the Big O notation comes in to play.
With binary search the worst case scenario is 𝛉(log2(n)), however, this is not the case 100% of the time as it is possible to find the target value on the first try which would make the runtime 𝛉(1). Therefore you can say that the runtime of binary search is never worse than 𝛉(log2(n)) but can be better. How would we write this using asymptotic notations, well we would write O(log2(n)).
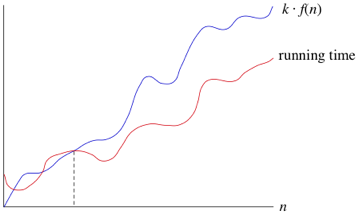
Like with the big theta notation once n becomes large enough it is less than or equal to k * f(n), the big O notation can be used. Of course the Big O notation can also be used on any function and not just a logarithmic function.
Big Omega Notation
Sometimes we instead want to say that a runtime will take at least a certain amount of time, but without providing an upper bound. This is where the big omega notation comes into play. This means any function where n becomes large enough and is greater than or equal to k * f(n).
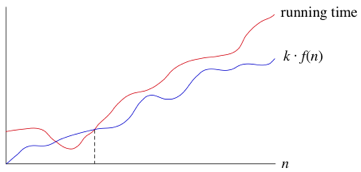
The Big Theta notation implies both Big O and Big Omega notations, but both Big O and Big Omega notations are imprecies due to not using both bounds. With this imprecision it is best to use Big Theta when describing a runtime of an algorithm.
No comments:
Post a Comment